The essence of my work can be put under the umbrella term categorical cybernetics, where lately I’ve specifically been focusing on categorical deep learning.

Most of these papers assume knowledge of category theory, most notably that of lenses/optics. If you’re new to category theory, check out the list of resources for learning category theory.

Categorical Deep Learning: An Algebraic Theory of Architectures

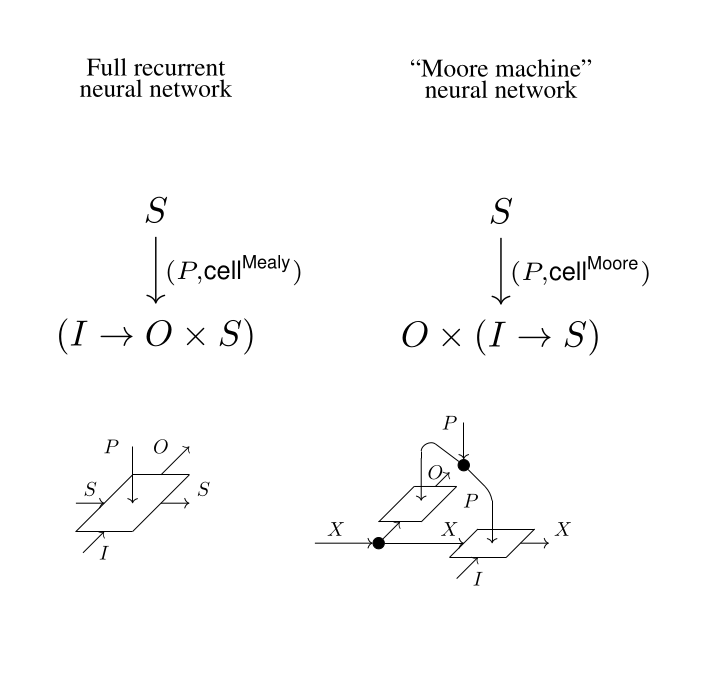
We propose category theory as a general-purpose language for specifying and understanding deep learning architectures. We use monad algebras to model equivariance of neural networks and thus capture the entirety of Geometric Deep Learning. By generalising monad to endofunctor algebras we remove the unnecessary constraint of invertibility and model structural (co)recursion, a concept otherwise only acknowledged in ad-hoc ways in deep learning. This consequently unlocks new vistas for enhancing capabilities of neural networks and our understanding of their internals.

My PhD Thesis

Deep learning, despite its remarkable achievements, is a young field. Like the early stages of many scientific disciplines, it is marked by the discovery of new phenomena, ad-hoc design decisions, and the lack of a uniform mathematical foundation. This thesis develops a novel mathematical foundation for deep learning based on the language of category theory. We develop a new framework that is end-to-end, unform, and prescriptive, covering backpropagation, weight sharing, architectures, and the entire picture of supervised learning in a rigorous and unambiguous mathematical formalism.

Graph Convolutional Neural Networks as Parametric CoKleisli morphisms

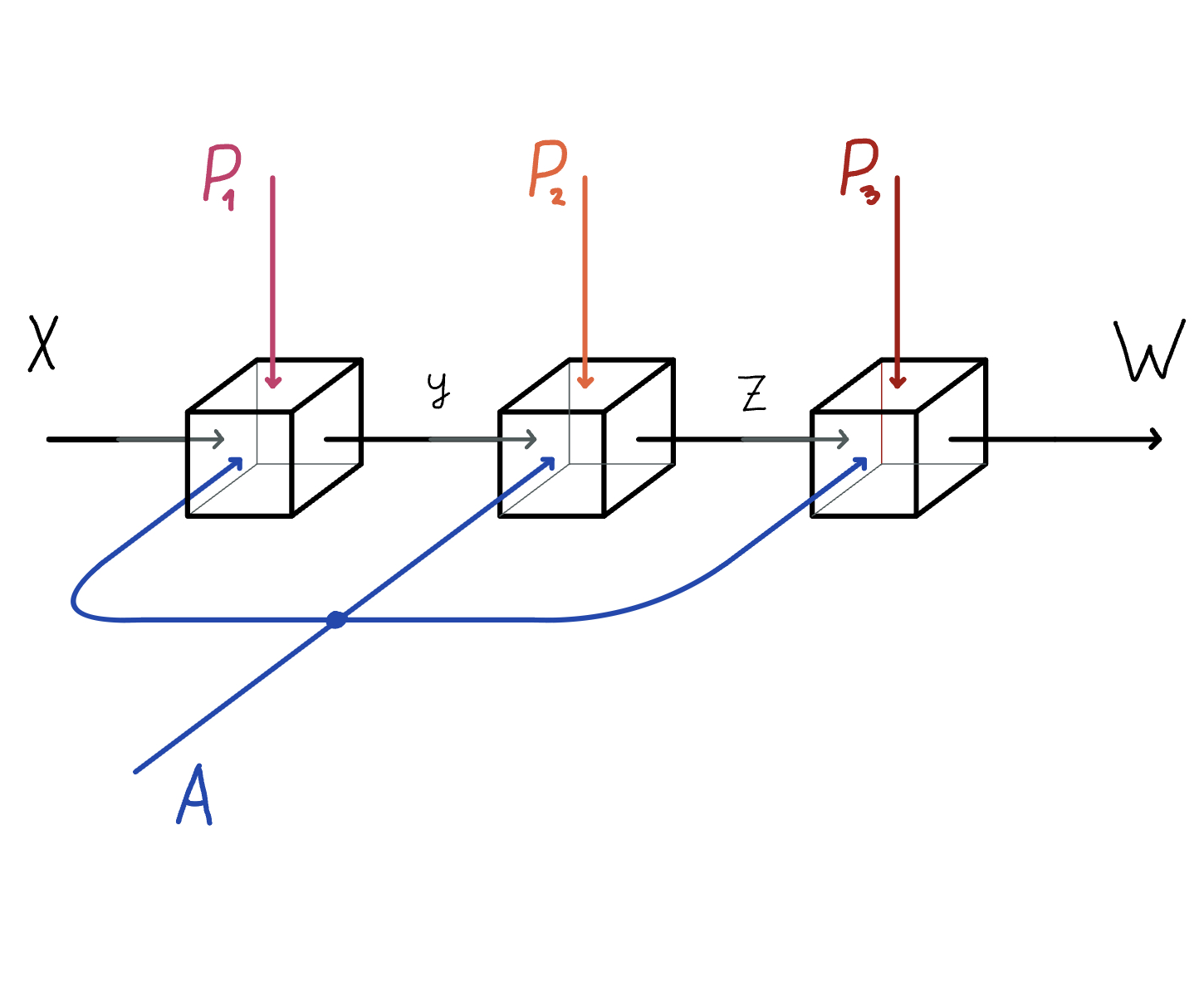
We define a bicategory of Graph Convolutional Neural Networks (GCNN). We factor it using our existing categorical constructions for deep learning: Para and Lens, but on a specific base category - the CoKleisli category of the product comonad. This gives us a high-level categorical account of a part of the inductive bias of GCNNs. Lastly, we hypothesize about possible generalisations of this categorical model to general message passing neural networks.

Space-time tradeoffs of lenses and optics via higher category theory

Optics and lenses are categorical gadgets modelling systems with bidirectional data flow. In this paper we observe that the denotational definition of optics – identifying two optics as equivalent by observing their behaviour from the outside – is not suitable for operational approaches where optics are not merely observed, but implemented in software with their internal setups in mind. We thus lift the existing categorical constructions and their relationships to the 2-categorical level, showing that the relevant operational concerns become visible.

Actegories for the Working Amthematician

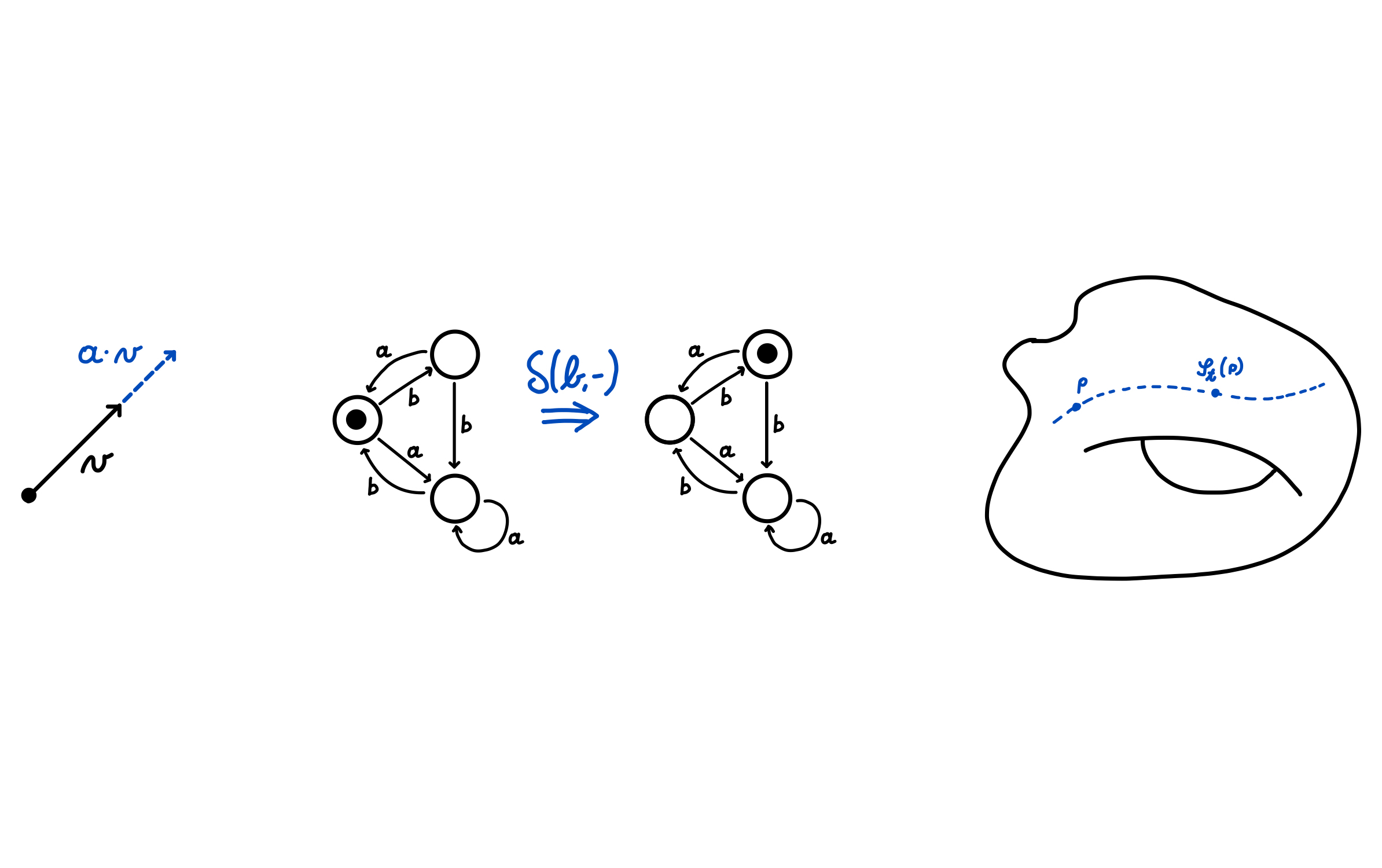
Playing on the name of a reference category theory textbook, this paper is a sizeable reference on the elementary theory of actegories, covering basic definitions and results. Motivated by the use of actegories in the theory of optics, the focus is on the way these actegories combine and interact with the monoidal structure.

Fibre Optics

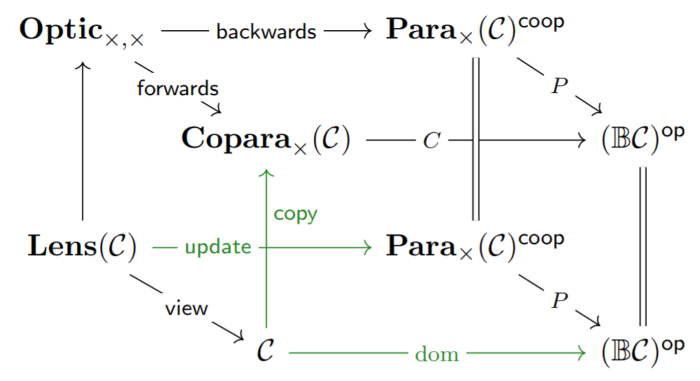
Lenses, optics and dependent lenses (equivalently morphisms of containers/polynomial functors) are all widely used in applied category theory as models of bidirectional processes. The goal of this paper is to unify these constructions in the framework of fibre optics.

Categorical Foundations of Gradient-Based Learning

We propose a categorical semantics of gradient-based machine learning algorithms in terms of lenses, parametrised maps, and reverse derivative categories. This foundation provides a powerful explanatory and unifying framework: encompassing a variety of neural networks, loss functions (including mean squared error and Softmax cross entropy), gradient update algorithms (including Nesterov momentum, Adagrad and ADAM). It generalises beyond the familiar continuous domains (modelled in categories of smooth maps) to the discrete setting of boolean circuits.

Towards foundations of categorical cybernetics

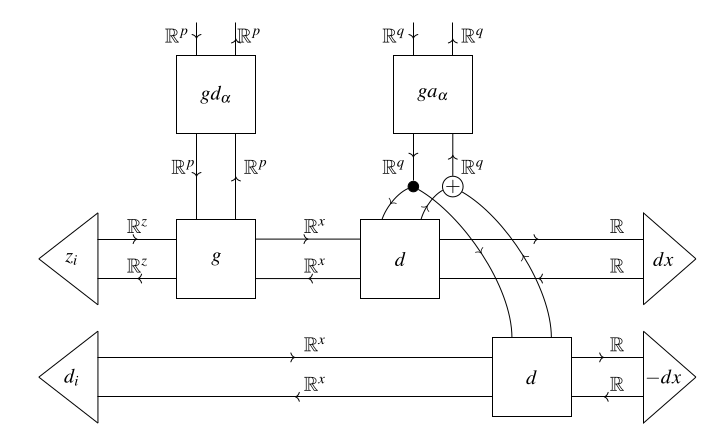
We propose a categorical framework for ‘cybernetics’: processes which interact bidirectionally with both an environment and a ‘controller’. Examples include open learners, in which the controller is an optimiser such as gradient descent, and open games, in which the controller is a composite of game-theoretic agents.

Category Theory in Machine Learning: a Survey

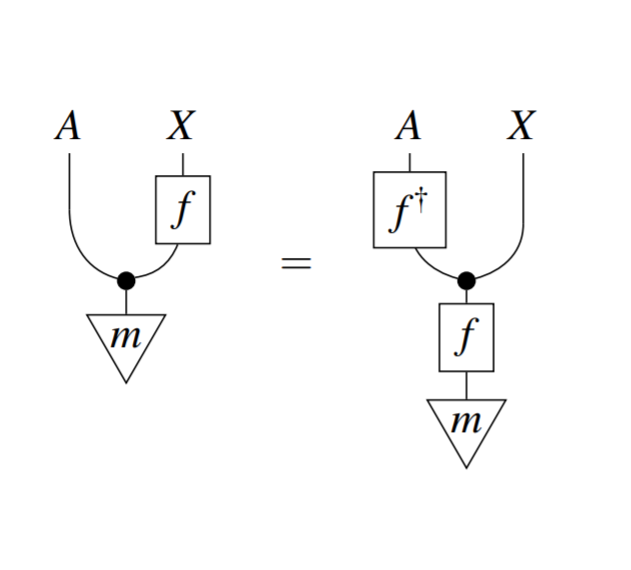
Over the past two decades machine learning has permeated almost every realm of technology. At the same time, many researchers have begun using category theory as a unifying scientific language, facilitating communication between different disciplines. It is therefore unsurprising that there is a burgeoning interest in applying category theory to machine learning. We document the motivations, goals and common themes across these applications, touching on gradient-based learning, probability, and equivariant learning.

Compositional Game Theory, Compositionally

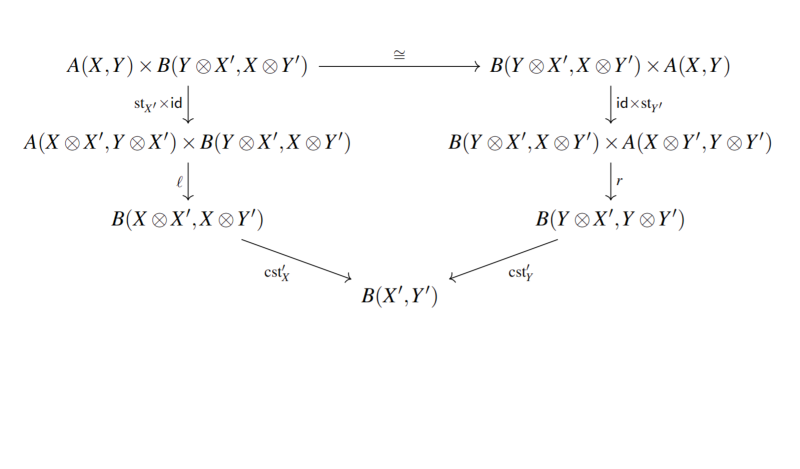
We present a new compositional approach to compositional game theory based upon Arrows, a concept closely related to Tambara modules. We use this compositional approach to show how known and previously unknown variants of open games can be proven to form symmetric monoidal categories.

Learning Functors using Gradient Descent

We build a category-theoretic formalism around a neural network system called CycleGAN, an approach to unpaired image-to-image translation. We relate it to categorical databases, and show that a special class of functors can be learned using gradient descent. We design a novel neural network capable of inserting and deleting objects from images without paired data and evaluate it on the CelebA dataset.