Graph Convolutional Neural Networks as Parametric CoKleisli morphisms

This is a short blog post accompanying the latest preprint of Mattia Villani and myself which you can now find on the ArXiv.

This paper makes a step forward in substantiating our existing framework described in Categorical Foundations of Gradient-Based Learning. If you’re not familiar with this existing work - it’s a general framework for modeling neural networks in the language of category theory. Given some base category with enough structure, it describes how to construct another category where morphisms are parametric, and bidirectional. Even more specifically - it allows us to describe the setting where the information being sent backwards is the derivative of some chosen loss function.

This is powerful enough to encompass a variety of neural network architectures - recurrent, convolutional, autoregressive, and so on. What the framework doesn’t do is describe the structural essence of all these architectures at the level of category theory.

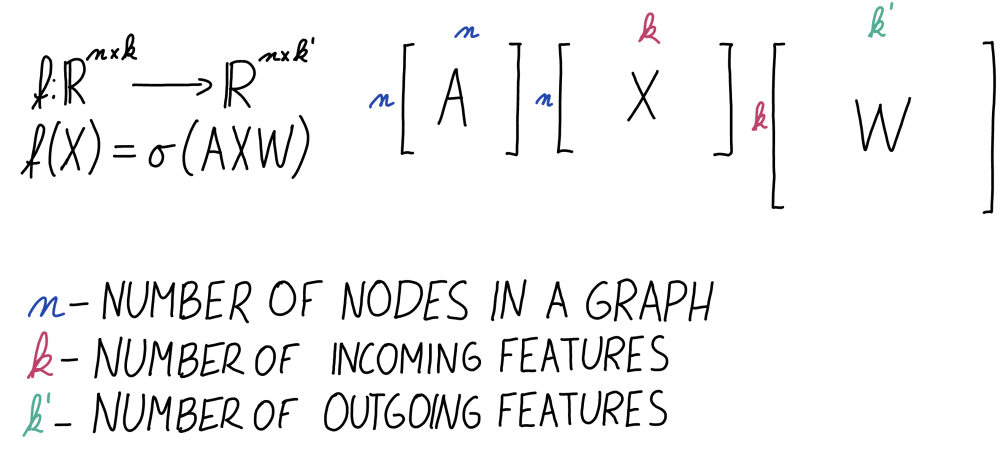
Our new paper does that, for one specific architecture: Graph Convolutional Neural Networks (GCNNs). We show that they arise as a morphisms for a particular choice of the base category - the CoKleisli category of the product comonad.

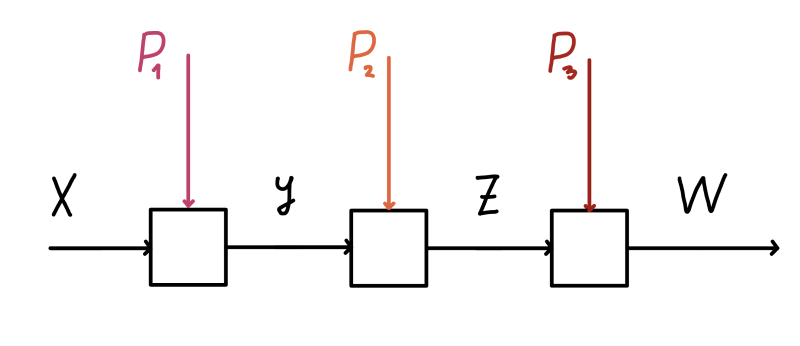
It’s a pretty straightforward idea. It’s based on the central observation that a GCNN layer has a different composition rule than just a regular feedforward layer. A simple feedforward layer is often thought of as a map , where is the weight matrix of that layer, and is some activation function. Then two layers are composed using the Para construction which defines a map (where is the weight matrix of the second layer). This is shown below, where we compose three such parametric maps (and use , , and to denote weight spaces).

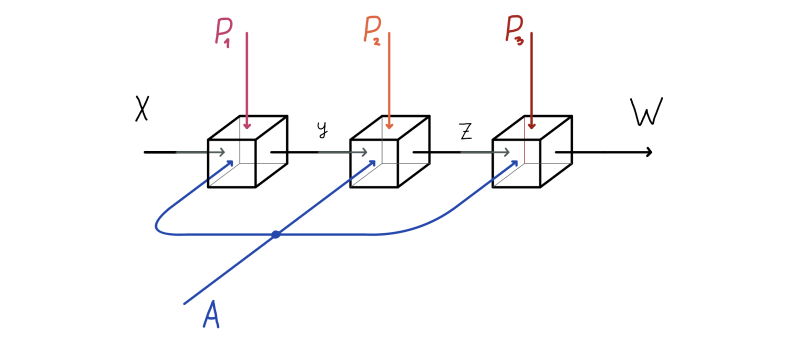
But a GCNN layer is different! It is defined as a function , where in addition to the weight matrix we also have the adjacency matrix of our underlying graph.

Crucially (and unlike with standard feedforward layers) here each layer shares the adjacency matrix. This means that when we compose two layers we obtain a composite morphism . Graphically, this is shown below, where we see a composition of three GCNN layers.

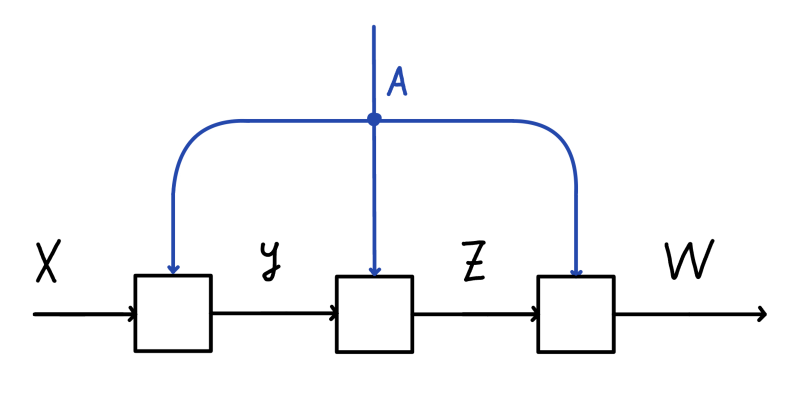
Note that here is globally accessible information for each layer, while and are layer specific. This means that we need a way to account for the global information, in addition to having Para account for the local one. Fortunately, there is a neat categorical construction that models just that – the already mentioned CoKleisli category of the product comonad on some base category . It’s defined for a particular object in our category (the space of adjacency matrices of a specific size) and its looks at coeffectful morphisms that have access to this information. It might sound complicated, but it has a simple graphical representation. Below we see a composition of three morphisms in this category.

We’ll denote this category by . (Un)surprisingly, it turns out that when the category has enough structure to do learning on it, so does . Which in turn means that all the constructions for parametric bidirectional morphisms from our original paper apply here as well! For instance, we can use the same kind of diagrams (drawn below) depicting a closed parametric lens whose parameters are being learned (from our original paper) for the base category , and draw string diagrams of GCNN learning!

I find this pretty exciting.

On the other hand, I see this paper merely as a stepping stone. It’s a neat idea - but there’s much more work to do. What’s making me deeply excited is where it could lead us further – to categorical models of full message passing Graph Neural Networks – and beyond.

Thanks to Ieva Čepaitė for a read-through of this post.